Modelado del comportamiento vibracional del modelo isotropico de la membrana timpanica.
La membrana timpanica es una estructura que se encuentra dentro de nuestro oido. El comportamiento de esa pequeña membrana puede ser modelado por la ecuación de onda:
\begin{equation} \frac{\partial^2 u}{\partial t^2}=c^2\frac{\partial^2u}{\partial x^2} \end{equation}
La ecuación, en este caso, se encuentra contenida en los siguientes parametros:
\begin{equation} 0<x<l\hspace{2mm} \land\hspace{2mm} 0<t<t_f \end{equation}
La condición de borde para nuestro sistema es:
\begin{equation} u(0,t)=u(l,t)=0 \hspace{2mm} \end{equation}
Y la condición inicial:
\begin{equation} \frac{\partial u_x^0}{\partial t}=0 \hspace{2mm}\land\hspace{2mm} u(x,0)=sin(\frac{n\pi x}{L}) \end{equation}
donde $n$ es el nodo vibracional. Los valores pueden ser $n=1,2,3,\cdots$ pero solamente observare los primeros cinco.
Los valores a utilizar para este sistema son:
- $L_T=4x10^{-5}m$ que sera el largo de la parte tensa.
- $L_f=1x10^{-4}m$ que sera el largo de la parte flácida.
- $t_0=0$
- $t_f=2.42x10^{-7}s$
- $E=2x10^7Pa$
- $\rho_T=1000kg/m^3$ siendo la densidad de la parte tensa.
- $\rho_f=1200kg/m^3$ siendo la densidad de la parte flácida.
- $\mu=0.3$ siendo el modulo de Poison.
En este caso, la velocidad de propagación $(c)$ es:
\begin{equation} c=\sqrt{\frac{E}{\rho}\frac{(1-\mu)}{((1+\mu)(1-2\mu))}} \end{equation}
Usare diferencias finitas para resolver la ecuación diferencial. Para el código, usare las siguientes librarias:
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from numba import njit
from jupyterthemes import jtplot
jtplot.style(theme='monokai')
Si te estas preguntando, ¿qué es Numba? Bueno, es una libreria de Python que hace que nuestro código sea mucho más rapido que antes. Puedes saber más sobre el aquí.
Ahora, pondre la sección donde creo las variables a usar.
lt=4e-5
lf=1e-4
tf=2.42e-7
E=2e7
rhot=1000
rhof=1200
mu=0.3
#Ahora, crea las variables c
ct=np.sqrt((E/rhot)*((1-mu)/((1+mu)*(1-2*mu))))
cf=np.sqrt((E/rhof)*((1-mu)/((1+mu)*(1-2*mu))))
#Se escoge el mallado de la ecuación
Nx=551
Nt=551
dxt=(lt)/(Nx-1)
dxf=(lf)/(Nx-1)
dt=(tf)/(Nt-1)
#Creamos los arreglos para x y t
xt=np.linspace(0,lt,Nx)
xf=np.linspace(0,lf,Nx)
t=np.linspace(0,tf,Nt)
@njit() #Creamos una función que calcule el criterio CFL
def cfl(c,dt,dx):
return c*(dt/dx)
#Ahora, lo calculamos
kt=cfl(ct,dt,dxt)
kf=cfl(cf,dt,dxf)
print('''The CFL condition is
kt={f}
kf={d}'''.format(f=kt,d=kf))
Esto me dice que $k_f=0.362$ y $k_t=0.99$. Como ambos criterios estan bien, puedo continuar.
Es tiempo de trabajar en la discretización de las ecuaciones. Podemos utilizar diferencias finitas y demostrar que las ecuaciones discretizadas son:
\begin{equation} \frac{\partial^2 u}{\partial x^2}\approx\frac{u_{x+1}^{t}-2u_{x}^{t}+u_{x-1}^{t}}{\Delta x^2} \end{equation}
\begin{equation} \frac{\partial^2 u}{\partial t^2}\approx\frac{u_{x}^{t+1}-2u_{x}^{t}+u_{x}^{t-1}}{\Delta t^2} \end{equation}
Por lo que, la PDE discretizada sera:
\begin{equation} \frac{u_{x}^{t+1}-2u_{x}^{t}+u_{x}^{t-1}}{\Delta t^2}=c^2\frac{u_{x+1}^{t}-2u_{x}^{t}+u_{x-1}^{t}}{\Delta x^2} \end{equation}
Usando algo de algebra, obtengo que:
\begin{equation} u_x^{t+1}=k^2(u_{x+1}^{t}+u_{x-1}^{t})+2u_{x}^{t}(1-k^2)-u_x^{t-1} \end{equation}
donde $k=c\frac{dt}{dx}$.
Esta ecuación puede ser programada. Pero primero, debere checar el primer paso de la simulación para poder calcular $u_x^2$ usando $u_x^1$ y $u_x^0$. Esto significa:
\begin{equation} u_x^1=k^2(u_{x+1}^{0}+u_{x-1}^{0})+2u_{x}^{0}(1-k^2)-u_x^{-1} \end{equation}
No conocemos el valor $u_x^{-1}$, ya que se encuentra afuera del dominio del tiempo y de nuestro mallado. ¿como podriamos calcularlo? Bueno, podemos calcularlo dsicretizad la nuestra condición inicial:
\begin{equation} \frac{\partial u_x^{0}}{\partial t}\approx\frac{u_x^1-u_x^{-1}}{\Delta t} \end{equation}
Sabemos por nuestra condición inicial que $\frac{\partial u_x^0}{\partial t}=0$, por lo que tenemos:
\begin{equation} u_x^{-1}=u_x^1 \end{equation}
Ahora, volviendo a la ecuación para calcular $u_x^1$, usamos esto que recién calculamos y con la ayuda de álgebra, tenemos:
\begin{equation} u_x^1=\frac{1}{2}k^2(u_{x+1}^{0}+u_{x-1}^{0})+u_{x}^{0}(1-k^2) \end{equation}
Ya tenemos todo para poder programar la solución.
Muchas gracias al libro Finite Difference Computing with PDEs escrito por Hans Petter Langtangen y Svein Linge.
Hice tres funciones en Python para el código. La primera (que es la siguiente) fue creada para usar el método de diferencias finitas.
@njit() #Function to execute finite difference method
def fdm(Nx,Nt,l,tf,k,x,t,n):
u=np.zeros((Nx,Nt))
u=BC(u,l,Nx,Nt) #First, we initialize the BC
u=IC(u,Nt,Nx,x,k,n,l) #And nowm we calculate the IC
for j in range(1,Nt-1):
for i in range(Nx-1):
u[i,j+1]=k**2*(u[i+1,j]+u[i-1,j])+2*u[i,j]*(1-k**2)-u[i,j-1]
u=BC(u,l,Nx,Nt)
return u
Otra para poder añadir la condicion inicial del sistema en mi solución.
@njit() #With this, we can calculate the initial conditions
def IC(u,Nt,Nx,x,k,n,l):
for j in range(1,Nx-2):
u[j,0]=np.sin(n*np.pi*x[j]/l)
#u[j,0]=np.sin(np.pi*x[i])+0.5*np.sin(3*np.pi*x[i])
for i in range(Nx-1):
u[i,1]=0.5*k**2*(u[i+1,0]+u[i-1,0])+u[i,0]*(1-k**2)
return u
Y la última para imponer las condiciones de borde.
@njit() #This is for the boundary conditions
def BC(u,l,Nx,Nt):
for j in range(Nt-1):
u[0,j]=0
u[Nx-1,j]=0
return u
Puedo resolver ahora el sistema para distintos $n$. La gráfica de nuestro sistema es:
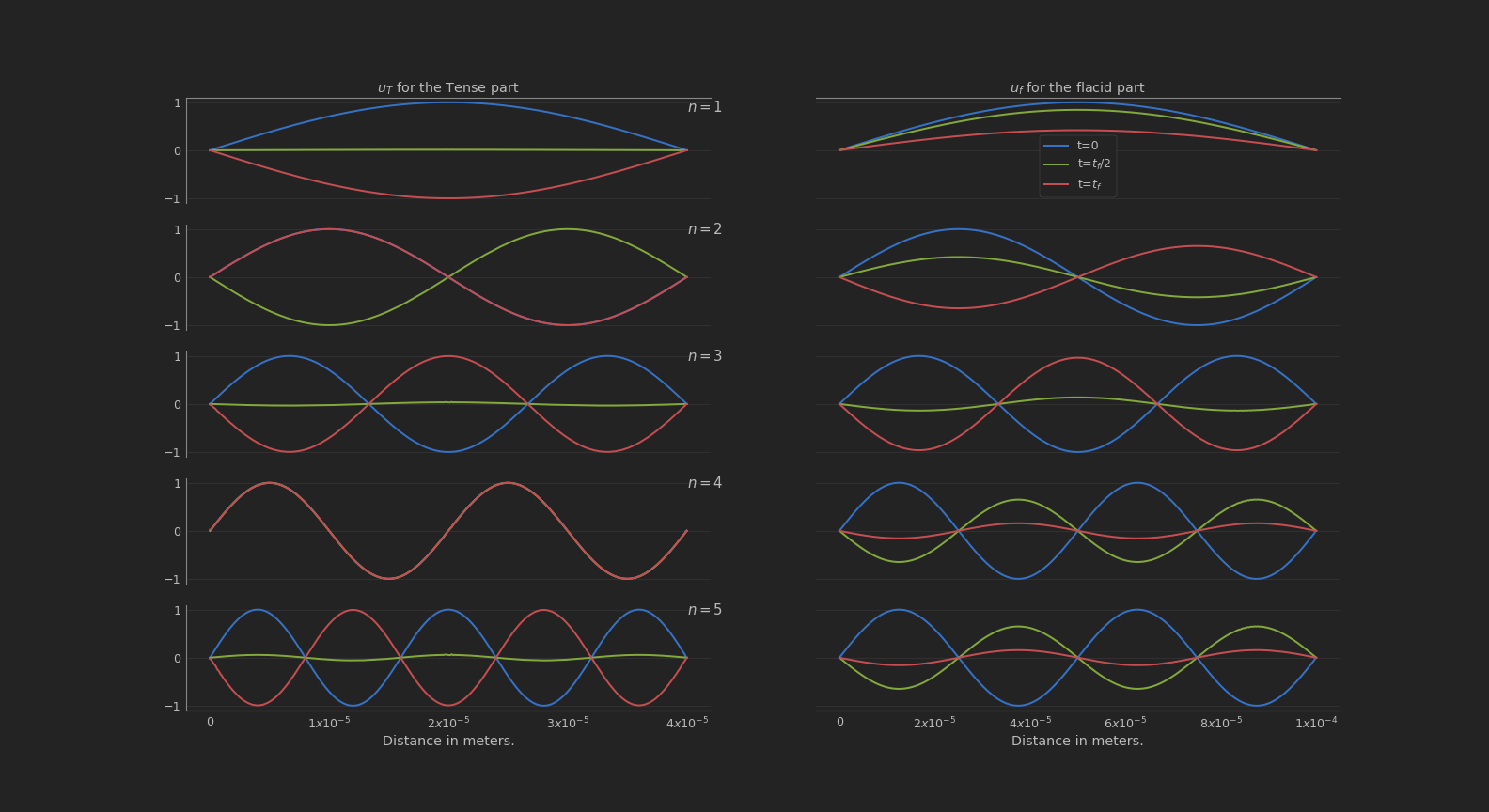
Como es una imagen estática, solo mostre los tiempos $t=0$, $t=\frac{t_f}{2}$ y $t=t_f$.
Para dar una idea mucho más clara de como se comporta el sistema a cualquier $t$, cree un video de la solución.
Observamos que ambas partes de la membrana se comportan de manera muy similar, pero con la membrana flácida teniendo más restricción de movimiento. No es dificil notar que tanto la parte tensa y flácida quieren comportarse igual pero se le dificulta a la parte flácida seguir el ritmo de la tensa.
Eso es todo por este post! Puedes ver el jupyter notebook de este problema aquí.